Netflix Artwork Personalization and EE Problem

An effective recommendation system does not only about the generating the recommendation result, but also exhibits it in a compelling approach. In the movie recommendation, it is not enough merely concentrating on optimizing the accuracy of recommendation. Why should users care about the movie? How do we convince users that such movie or TV series is worth watching? A company providing media services will obtain more profits and attention if the approach of displaying recommendation is carefully devised.

In the media recommendation system (movie or TV show), most of the movies are displayed with their artwork covers. Users can gain more knowledges from the posters than simply from a title. The starring actors/actresses or the category of the movie may trigger the user to watch it, and these information could not be acquired from titles only. If we show the user exactly what intriguing about the movie or TV show, the user tends to click and watch it. Therefore, if displaying the artwork of the media properly, it will significantly attract users’ interests and maximize their satisfaction.

The Netflix researchers and engineers apply personalization on the artwork and covers. When entering into the Netflix platform, different users might receive diverse artwork in the exactly same TV show.

Netflix edits several covers for each media, but exploring the best artwork for each user will be challenging. The system should find the user’s preference carefully without exerting too much negative effect and exploit the preference as much as possible. This is denoted as the traditional recommendation problem: exploration and exploitation. I will discuss about the technical background about this issue and apply it in the real-life Netflix application.

Background

The recommendation method targets at maximizing user’s engagement and preventing unsatisfied result. When the system always exploits the preference of the user, user tends to get bored since the system invariably recommends the similar contents. If system keeps exploring, users might be unsatisfied when receiving the disliked items. Therefore, the EE problem in recommender system is a trade-off problem, and the bandit algorithm can balance this two issues.

(Bandit methods with exploit, ignore and explore. From James McInerney, et al.)

Bandit Algorithm Setting

Bandit algorithm is an effective approach to solve EE problem in recommender system. This algorithm is a set of methods to solve multi-armed bandit (MAB) problem, a classic problem in probability theory. MAB is a multiple slot machines with unknown reward distribution. A gambler can play one arm at a time. To fulfil maximum profit, the gambler ought to explore and exploit wisely, and various algorithms are designed to solve this problem, including $\epsilon$-Greedy algorithm, UCB, Thompson sampling, etc.

Before we go into the detail of each algorithm, we need to establish the basic bandit algorithm setting. In each round, the learner should choose an action, and the environment provides a feedback for this action. Every updates, learner should maximize the total reward, in other word, minimize the cumulative regret. The regret is denoted as the difference between optimal action and chosen action. And the cumulative regret can be represented as: $$ R_T=\sum_{i=1}^{T}(w_{opt}-w_{B(i)}) $$ while $w_{opt}$ is the optimal action, and $w_{B(i)}$ is the chosen action.

ε-Greedy Algorithm

The ε-greedy algorithm is a very simple bandit algorithm also denoted as naïve exploration which add a noise to the greedy policy. In this algorithm, assign $\epsilon$ a very small number between 0 to 1. The learner chooses the action with the best reward so far (exploitation) in $1-\epsilon$ possibility, and choose one action uniformly at random (exploration) with probability $\epsilon$.

This algorithm is better than the random-selecting algorithm since it modifies with the changes of item rewards. In addition, it is very simple to implement and costs little computational resources. However, since this algorithm does not utilize the historical records but still randomly select in the exploration process, the cumulative regret is unbounded.

Thompson Sampling Algorithm

The Thompson sampling is a probability method which explores the profit probability distribution for each arm. Most of time, we apply beta distribution to find the probability. Please refer to this blog for the interpretation of beta distribution.

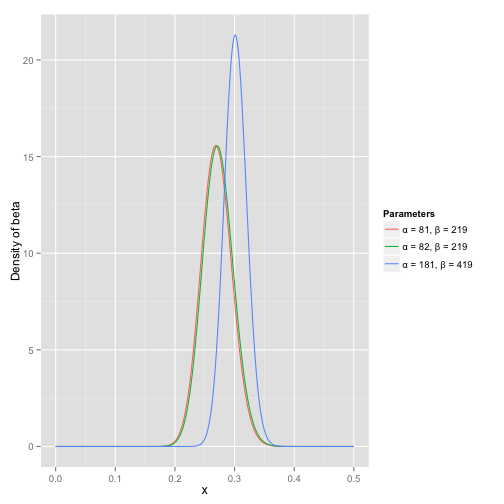
Generally, the beta distribution represents probability distribution, which is a perfect method to explore the profit of each arm. There is two possibility for each action, hit or miss, and the beta distribution is represented by $\text{Beta}(\alpha_0,\beta_0)$ initiating a curve. After several rounds of experiments, the two parameters modify, which is represented as $\text{Beta}(\alpha_0+\text{hits},\beta_0+\text{misses})$. As demonstrated in the following graph, with increasing attempts, the curve is getting thinner, and we can have a better chance finding the real possibility.

Upper Confidence Bound

Another effective algorithm is the upper confidence bound algorithm (UCB). This algorithm makes fully advantage of the historical information. First, we compute the average score of each arm $\bar{x_j}(t)$. The UCB is optimistic that always choose action with the higher $\alpha$-percentile. We use the following formula to select the arm with highest score: $$ S(t)=\bar{x_j}(t)+\sqrt{\frac{2\ln t}{T_{j,t}}} $$ while $t$ is the total attempt times, and $T_{j,t}$ is the # of how many times the arm has been tested.

MAB in Netflix Artwork Personalization

As we discussed previously, the artwork of a media is essential to appeal users. However, it is challengeable to recommend the cover properly. A good image should be representative, informative but avoid clickbait. It should also be engaging and differential [1].

The traditional recommendation approaches, e.g. collaborative filtering, might encounter several issues in this set of issue. Since it is imperative to respond quickly to user’s feedback, the computational cost of CF is expensive. In the media recommendation, we need a continuous and fast learning algorithm.

The Netflix applies bandit algorithm in artwork recommendation. We can establish the bandit algorithm setting by identifying the learners as artwork selector, environment as Netflix homepage, action as image for show and reward as the users with positive engagement. For the bellowing example, our purpose is to recommend an artwork of house of cards from three images. For each image, we have the history records from other uses. Then we can apply the MAB algorithm, in this example, upper confidence bound (UCB) algorithm, to make the recommendation for the next users. In the first picture, there is four attempts out of 12 attempts in total, with one successful attempt. After substituting the value, we can get $\frac{1}{4}+\sqrt{\frac{2\ln{12}}{4}}$. Similarly, we can calculate the value in the second and third pictures, which is $\frac{3}{5}+\sqrt{\frac{2\ln{12}}{5}}$ and $\frac{1}{3}+\sqrt{\frac{2\ln{12}}{3}}$, respectively. Finally, we select the second picture since it obtains the highest score.

(Example of Netflix artwork recommendation using UCB algorithm)

Essentially, Netflix applies this set of algorithm to make artwork recommendation. However, the algorithm above can not fulfill personalization according to different context. The only evidence we follow is the historical records from other users. Therefore, we need to introduce other features, like time, country, user’s preference, etc. Then this problem becomes a supervised leaning, since the input is the context, the output is the user’s action, and the feedback is the reward on whether the user clicks or not. Still using the previous example as the demonstration, we still want to recommend one of the images. Yet, we encompass some context features and use a supervised regression model to predict reward for each image. Then, we pick image with the highest predicted reward and use it as the recommendation.

(Example of Netflix artwork recommendation using LinUCB algorithm)

From the Netflix testing result, the contextual bandit approach helps with the user’s satisfaction compared to random selection or non-contextual bandits.

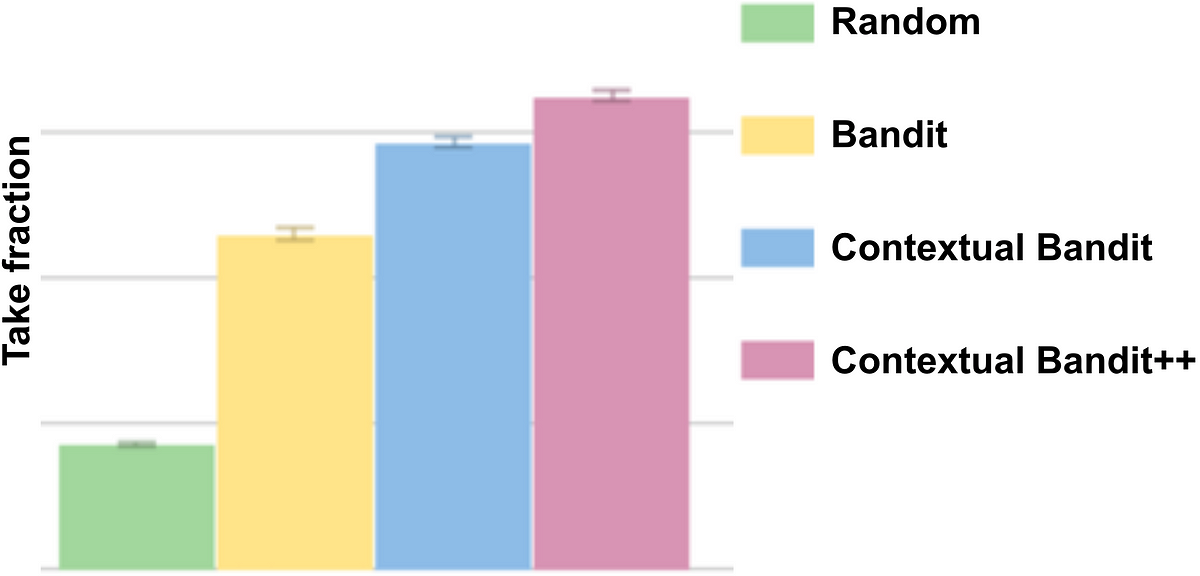
(Average image take fraction for different algorithms, from Netflix report [1])

Contradiction & Challenges

Netflix provides one of the best personalized recommendation services around the world, and it prompts the company’s revenue significantly. However, if the personalization goes too far, it can result in the creepiness. Users might worry about whether their privacy are invaded, and it will decrease the user’s satisfaction of the system.

In addition, the artwork recommendation should avoid clickbait, which means the information presented is not related or represents the title. If in this case, users might be upset since the movie is contradict to what they expect.

Unfortunately, even if Netflix obtains tremendous experiences in making personalized recommendation, they still get criticized by the public. According to Stacia Brown, she accused Netflix to reveal racial in recommendation. As a black lady, she received images with black cast members, but actually most of these actors/actress are merely minor characters in the series. After putting this question onto the twitter, several users confirm her suspicion.

Since recommending items based on the race is discrimination, this issue is alarming. First, feeding images on the same races tends to compel the user to watch the film. It should be the quality and the content of the show that drive audiences to watch, instead of the race. Second, users might feel creepy since it is hard to know how Netflix identifies the user’s race. Users might be afraid of the privacy invasion from those companies. Third, showing irrelevant images results in the clickbait. The audience might chase for the black actor, but in the end, that actor only shows less than ten cumulative minutes. Users might feel to be fooled and the satisfaction of the system is compromised.

Conclusion

To sum up, personalized artwork contributes to the enhancement of user experience. When this issue is handled properly, it can facilitate people to decide which shows to watch. This problem can also be defined as a classical explore and exploit problem. In this blog, I discuss three MAB algorithms to cope with the traditional EE problem. In addition to provide personalized experience, the real-world Netflix system converts this problem into the multiple supervised learning models, and selects the highest predicting rewards as well as recommend the picture to the user.

However, an excessive individualized system is inclined to result in the creepiness. The Netflix artwork recommendation is accused to be racial since it recommends various images according to different races. In my opinion, it is not the bias from Netflix but the algorithm’s fault. In the future, Netflix should adjust and maintain an equitable system for all users. Besides the system prejudice, this recommender system can also improved in several aspects. For example, currently those artwork are edited manually by designers, which is costly and time consuming. With the techniques of computer vision, Netflix can try to edit the image automatically based on the preference of users.

Acknowledge

This blog is adapted from the case study report on recommender system, CPS 4981, WKU.

Reference

[1] Ashok Chandrashekar, Fernando Amat, Justin Basilico and Tony Jebara. “Artwork Personalization at Netflix”. The Netflix Tech Blog. Dec 8, 2017

[2] Justin Basilico, PowerPoint of “ Artwork Personalization at Netflix”

[3] Joe Berkowitz, “ Is Netflix racially personalizing artwork for its titles?”. Fast Company. Oct 18, 2018

[4] McInerney, James, Benjamin Lacker, Samantha Hansen, Karl Higley, Hugues Bouchard, Alois Gruson, and Rishabh Mehrotra. “ Explore, exploit, and explain: personalizing explainable recommendations with bandits.” In Proceedings of the 12th ACM Conference on Recommender Systems, pp. 31-39. ACM, 2018.