[Introduction to Algorithm] Quick Sort

Quick sort is a widely applied sorting algorithm in the industry. It is a simple but very powerful algorithm that we should definetely understand. An interesting graph shown below can illustrate the process of this algorithm.

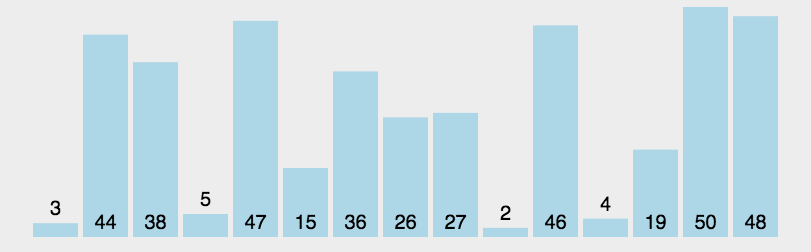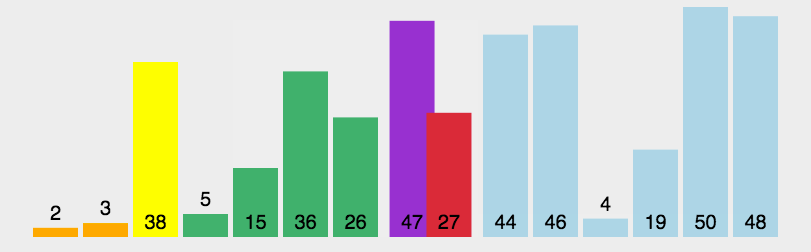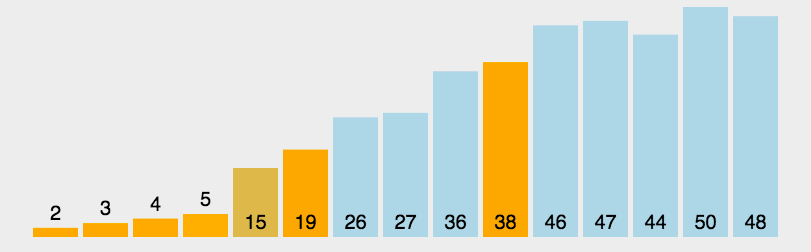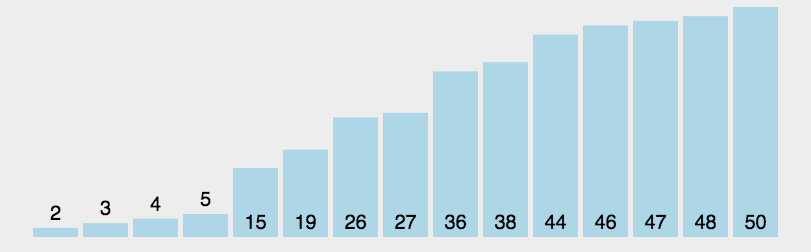
QuickSort

Implementation

def QUICKSORT(A, p, r):
    if p < r:
        q = PARTITION(A, p, r)
        QUICKSORT(A, p, q-1)
        QUICKSORT(A, q+1, r)

Partition

• Output: elements in the left is less than pivot (p), in the right is larger than pivot (p).
• Each time, put elements <= p in the left >= in the right
• Exchange the partition value and pivot

def PARTITION(A, lo, hi):
    # pivot p = A[hi] 
    p = A[hi]
    i = lo - 1
    for j in range(lo, hi-1):
        if A[j] <= p:
            i = i + 1
            A[i], A[j] = A[j], A[i]
    A[i+1], A[hi] = A[hi], A[i+1]
    return i+1

• Two cases for iteration of procedure PARTITION

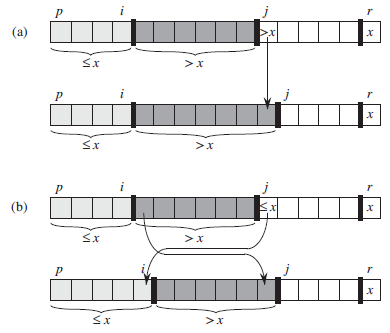
1537942239896

Another Approach

private static int partition(int[] A, int lo, int hi) {
    int i = li, j = hi;
    // pivot p = A[lo]
    int p = A[lo];
    while (true) {
        while (A[++i] < p)  if (i == hi) break;
        while (p < A[--j])  if (j == lo) break;
        if (i >= j) break;
        exch(A, i, j);
    }
    // exchange the pivot with the partition value
    exch(A, lo, j);
    return j;
}

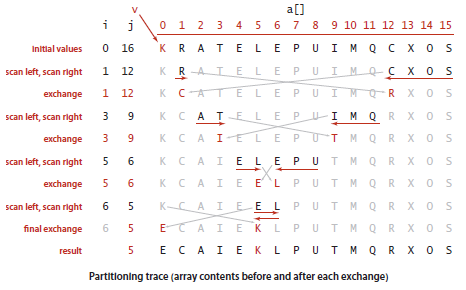
1537971744419

Analysis

Worst Case

• each element is larger or smaller than the pivot

\[ \begin{array}{l} T( n) \ =\ T( n-1) \ +\ T( 0) \ +\ \theta ( n)\\ =\ T( n-1) \ +\ \theta ( n)\\ =\ \theta \left( n^{2}\right) \end{array} \]

Best Case

• Partition produces two equal subproblems, each of size no more than n/2

\[ T( n) = 2T( n-1) + \theta( n) = \theta( n) \]

Expected Running Time

First of all, when we pick the pivot, we perform \(n-1\) comparisions.

Then, depending on the pivot, we might split the array into a LESS of size 0 and a GREATER of size \(n-1\); LESS of size 1 and a GREATER of size \(n-2\). All of these are equally likely with probability \(1/n\) each.

\[ T( n) \ =\ ( n-1) \ +\ \frac{1}{n}\sum ^{n-1}_{i=0}( T( i) +T( n-i-1)) \]

\[ T( n) \ =\ ( n-1) \ +\ \frac{2}{n} \ \sum ^{n-1}_{i=0} T( i) \]

Then we apply induction hypothesis, we assume \(T( n) \ \leqslant \ n \lg n\)