Two steps in Hash Table
- Compute the hash function
- Fix the collision resolution (algorithms and data to handle two keys that hash to the same index)
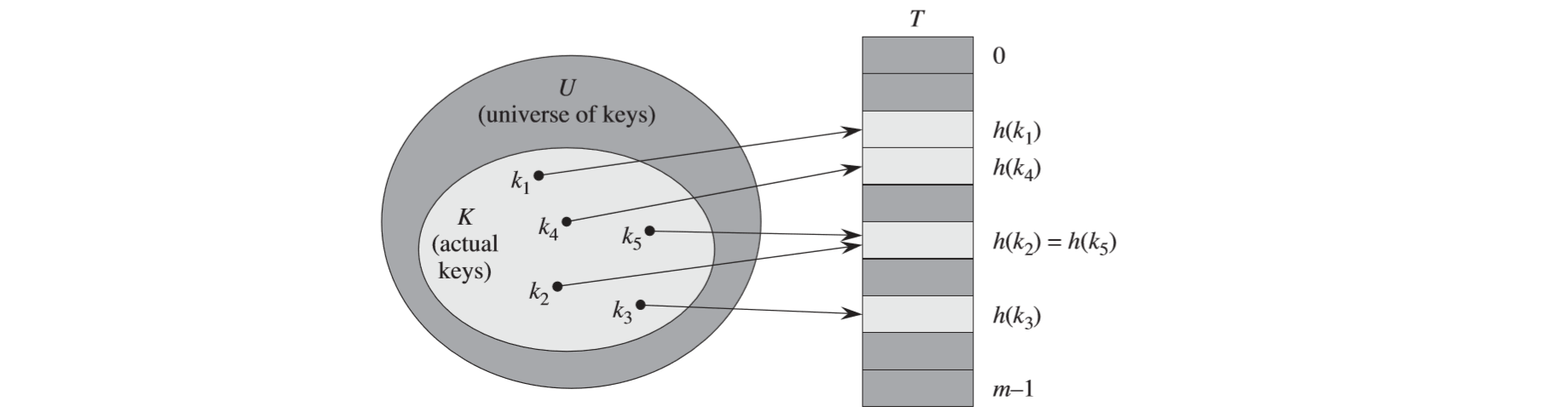
Hash functions
What is a good hash function?
- We scramble the keys uniformly.
- Efficiently computable
- Each table position equally likely for each key
- We expect to be independent of any patterns that might exist in the data
The division method
The hash function can be
\[ h(k)={k}\mod{m} \]
- A prime not too close to an exact power of 2 is a good choice for \(m\).
The multiplication method
The hash function can be
\[ h( k) =\lfloor m( kA\bmod 1)\rfloor \]
while
\[ kA\bmod 1=kA-\lfloor kA\rfloor \]
\(m\) is any value of m, typically to be a power of 2:
\[ m = 2^p \]
According to Knuth,
\[ A\approx \frac{\sqrt{5} -1}{2} \]
Java hashCode()
public int hashCode(String s) {
int hash = 0;
for (int i = 0; i < s.length; i++)
hash = s[i] + (31 * hash);
return hash;
}Matematically, the hash function is
\[ h(x)=\sum_{i=0}^{L=x.length}31^{L-1-i}\cdot x[i] \]
Collision Resolution
Chaining solution
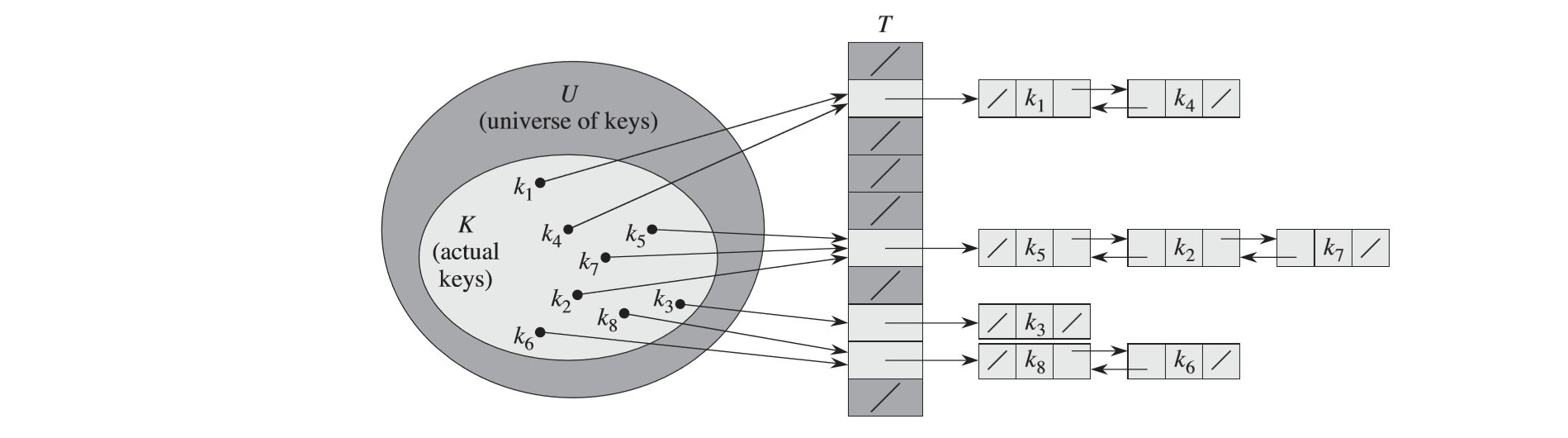
Analysis
Given a hash table \(T\) with \(m\) slots that stores \(n\) elements.
- load factor: \(\alpha=n/m\) (average number of elements stored in a chain)
For \(j=0,1,...,m-1\), denote the length of the list \(T[j]\) by \(n_j\), so that the expected time to find \(n_j\) is \(E[n_j]=\alpha=n/m\).
Theorems
- In a hash table (chaining), an unsuccessful search takes average-case time \(\Theta(1+\alpha)\).
- In a hash table (chaining), a successful search takes average-case time \(\Theta(1+\alpha)\)
Proof:
Let \(x_i\) denote the \(i\)th element inserted into the table, for \(i=1,2,...n\), and let \(k_i=x_i.key\).
For \(k_i\) and \(k_j\), we define the indicator random variable \(X_{ij}=I\{ h(k_i)=h(k_j)\}\).
Then, we have \(Pr\{ h(k_i)=h(k_j)\}=1/m\), and \(E[X_{ij}=1/m]\).
Thus, the expected number of elements examined in a successful search is:
\[ \begin{equation} \begin{aligned} &E\left[\frac{1}{n}\sum ^{n}_{i=1}\left( 1+\sum ^{n}_{j=i+1} E[ X_{ij}]\right)\right] \newline &=\frac{1}{n}\sum ^{n}_{i=1}\left( 1+\sum ^{n}_{j=i+1}\frac{1}{m}\right) \newline &=1+\frac{1}{nm}\sum ^{n}_{i=1}( n-i)\newline &=1+\frac{1}{nm}\left(\sum ^{n}_{i=1} n-\sum ^{n}_{i=1} i\right)\newline &=1+\frac{1}{nm}\left( n^{2} -\frac{n( n+1)}{2}\right)\newline &=1+\frac{n-1}{2m}\newline &=1+\frac{\alpha }{2} -\frac{\alpha }{2n} \end{aligned} \end{equation} \]
\[ \therefore \Theta(2+\alpha/2-\alpha/2n)=\Theta(1+\alpha) \]
In average: \(O(1)\)
Open Addressing
- Use an array of size \(M >> N\) (typically \(M=2N\))
- Hashing: map key to integer i between 0 to M-1
- Probe sequence
- for every key k, the probe sequence: \(<h(k,0),h(k,1),...,h(k,m-1)>\)
Linear probing
\[ h(k, i) = (h^\prime (k)+i)\mod{m} \]
- Insert: put in slot \(i\) if free; otherwise try \(i+1\), \(i+2,\) etc.
- Search: search slot \(i\); if occupied but not match, try $ i+1$, \(i+2\), etc.
primary clustering
This means that long runs of occupied slots build up, increasing the average search time. Clusters arise and make the occupied slots get longer and longer.
Quadratic probing
\[ h(k,i)=(h^\prime (k)+c_1i+c_2i^2)\mod m \]
Drawback
- The property leads to a milder form of clustering, called secondary clustering.
Double hashing
\[ h(k,i)=(h_1(k)+ih_2(k))\mod m \]
while
\[ h_1(k)=k\mod m \]
\[ h_2(k)=p-(k\mod p) \]
(\(p\) is a prime similar to \(m\))
Analysis
- Given an open-address hash table with load factor \(\alpha=n/m < 1\), the expected number of probes in an unsuccessful search is at most \(1/(1-\alpha)\).
- Inserting an element into an open-address hash table with load factor \(\alpha\) requires at most \(1/(1-\alpha)\) probes on average.
Proof:
- probability first probe successful: \(\frac{m-n}{m}\)
- if first probe fails, probability of second probe successful: \(\frac{m-n-1}{m-1}\)
- if 1st &2nd probe fails, probability of second probe successful: \(\frac{m-n-2}{m-2}\)
- ...
Therefore, the total probability of unsuccessful search for \(i\) is: \[ \begin{equation} \begin{aligned} Pr\{X\} &=\frac{n}{m} \cdotp \frac{n-1}{m-1} ...\cdotp \frac{n-i+2}{m-i+2}\\ &\leqslant \left(\frac{n}{m}\right)^{i}\\ &=\alpha ^{i} \end{aligned} \end{equation} \]
\[ \begin{equation} \begin{aligned} \therefore E[ X] &=\sum ^{m-1}_{i=0} Pr\{X\}\\ &\leqslant \sum ^{m-1}_{i=0} \alpha ^{i}\\ &=\frac{1}{1-\alpha } \end{aligned} \end{equation} \]
- Given an open-address hash table with load factor \(\alpha < 1\), the expected number of probes in a successful search is at most \(\frac{1}{\alpha}\ln{\frac{1}{1-\alpha}}\).
Proof: the expected number of probes in a search for k is at most \(1/(1-i/m) = m/(m-i)\).
Therefore,
\[ \begin{equation} \begin{aligned} \frac{1}{n}\sum ^{n-1}_{i=0}\frac{m}{m-i} \ &=\frac{m}{n}\sum ^{n-1}_{i=0}\frac{1}{m-i}\\ &=\frac{1}{\alpha }\sum ^{m}_{k=m-n+1}\frac{1}{k}\\ &\leqslant \frac{1}{\alpha }\int ^{m}_{m-n}( 1-x) dx\\ &=\frac{1}{\alpha }\ln\frac{m}{m-n}\\ &=\frac{1}{\alpha }\ln\frac{1}{1-\alpha } \end{aligned} \end{equation} \]