This blog is my first post of the course note of the classical textbook, Introduction to Algorithm. Many graphs and formulas might be directed retrieved from this book. Some other blogs might utilize the book Algorithms, 4th and other open source online with proper citation.

This series of blog is only for the learning purpose. Please inform me if violating any copyright issue.

Chapter 2 Basic Analysis

Loop invariant

Properties which remain the same in the whole iterating process.
It could testify the correctness of algorithm.
It should be satisfied in the following three conditions:
Initialization: It is true before the first iteration
Maintenance: If it is true after the n's iteration, it should remain true before the (n+1)'s iteration
Termination: The terminational condition of the iteration should be false

Simple Sorting Algorithms

Selection sort

Select the smallest one and put into the first .

Insertion Sort

Insert the number into a sorted queue

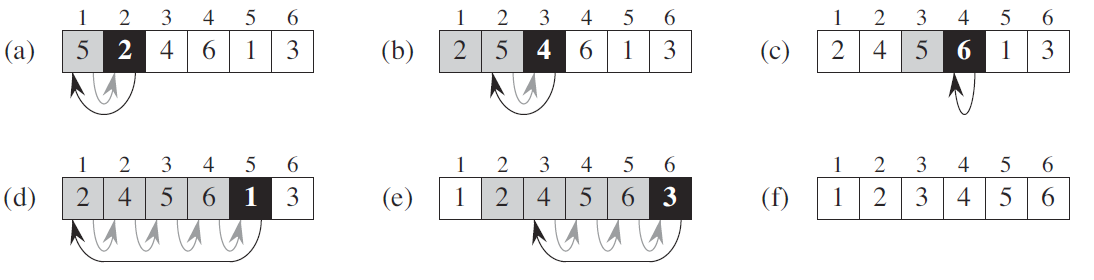
The Principles of Analyzing Algorithm

No concurrent operation
Some computational costs can be ignored
Precision is not important when analyzing the algorithms

Chapter 3 Growth of Functions

Asymptotic notations

\(\Theta\)-Notation

\[ \Theta(g(n))=\{f(n):\text{ there exist positive constants }c_1,c_2,\text{ and } n_0 \text{ such that }\\0\le c_1g(n)\le f(n)\le c_2g(n) \text{ for all } n \ge n_0\} \]

\(O\)-Notation

\[ O(g(n))=\{f(n):\text{ there exist positive constant }c,\text{ and } n_0 \text{ such that }\\0\le f(n)\le cg(n) \text{ for all } n \ge n_0\} \]

\(\Omega\)-Notation

\[ \Omega(g(n))=\{f(n):\text{ there exist positive constant }c,\text{ and } n_0 \text{ such that }\\0\le cg(n)\le f(n) \text{ for all } n \ge n_0\} \]

\(o\)-Notation

\[ o(g(n))=\{f(n):\text{ for any positive constant }c>0,\text{ there exits a constant }\\n_0 >0 \text{ such that }0\le f(n)< cg(n) \text{ for all } n \ge n_0\} \]

We have:

\[ lim_{n\to \infty}=\frac{f(n)}{g(n)}=0 \]

\(\omega\)-Notation

\[ w(g(n))=\{f(n):\text{ for any positive constant }c>0,\text{ there exits a constant }\\n_0 >0 \text{ such that }0\le cg(n) < f(n) \text{ for all } n \ge n_0\} \]

We have:

\[ lim_{n\to \infty}=\frac{f(n)}{g(n)}=\infty \] ### Summary

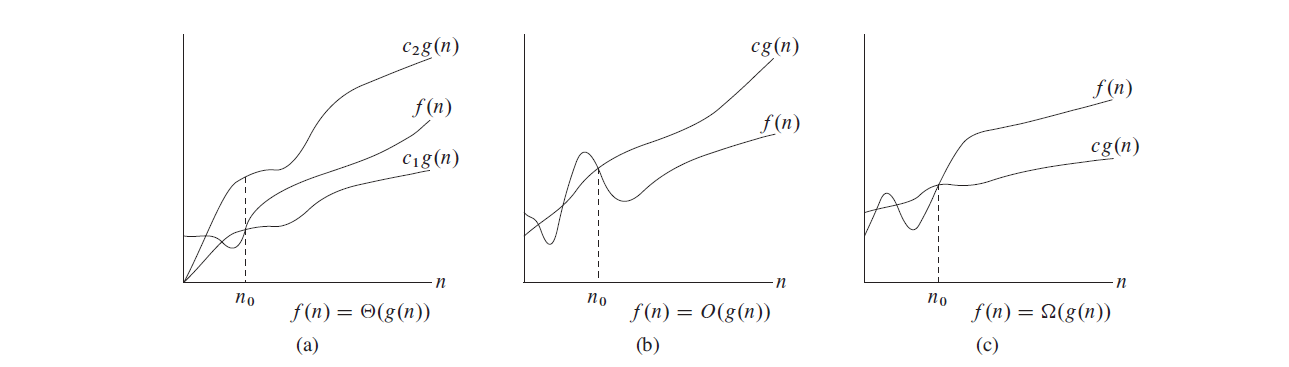
Standard notations

Monotonicity

monotonically increasing: if m ≤ n implies f(m) ≤ f(n).

monotonically decreasing: if m ≤ n implies f(m) ≥ f(n).

strictly increasing: if m < n implies f(m) < f(n).

strictly decreasing: if m < n implies f(m) > f(n).

Chapter 4 Divide and Conquer and Analysis

Recurrences

There are three methods which could determine the asymptotical bonds.

Substitutions method

We guess a bound and then apply induction to prove the correctness of our guess. (Refer to section 4.3 for more information)

recursion-tree method

Consider a recurrence \(T(n)=3T(n/4)+\Theta(n^2)\).

We can apply the recursion tree:

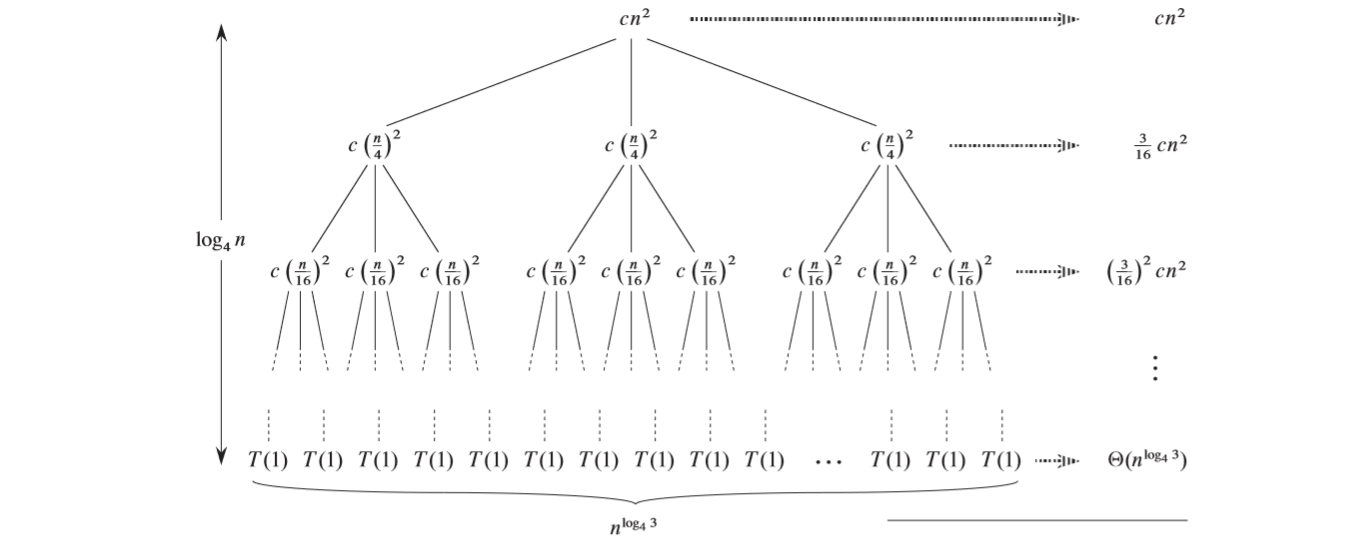
1544181457372

Then we add up the costs over all levels, finally we will come up the result that \(T(n)=O(n^2)\). (Omit the mathematic deduction process, please refer to section 4.4)

master method

1536644230277

Maximum Subarray

# Code from geeksforgeeks
# Available at: https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/ 

# A Divide and Conquer based program 
# for maximum subarray sum problem 
  
# Find the maximum possible sum in 
# arr[] auch that arr[m] is part of it 
def maxCrossingSum(arr, l, m, h) : 
      
    # Include elements on left of mid. 
    sm = 0; left_sum = -10000
      
    for i in range(m, l-1, -1) : 
        sm = sm + arr[i] 
          
        if (sm > left_sum) : 
            left_sum = sm 
      
      
    # Include elements on right of mid 
    sm = 0; right_sum = -1000
    for i in range(m + 1, h + 1) : 
        sm = sm + arr[i] 
          
        if (sm > right_sum) : 
            right_sum = sm 
      
  
    # Return sum of elements on left and right of mid 
    return left_sum + right_sum; 
  
  
# Returns sum of maxium sum subarray in aa[l..h] 
def maxSubArraySum(arr, l, h) : 
      
    # Base Case: Only one element 
    if (l == h) : 
        return arr[l] 
  
    # Find middle point 
    m = (l + h) // 2
  
    # Return maximum of following three possible cases 
    # a) Maximum subarray sum in left half 
    # b) Maximum subarray sum in right half 
    # c) Maximum subarray sum such that the  
    #     subarray crosses the midpoint  
    return max(maxSubArraySum(arr, l, m), 
               maxSubArraySum(arr, m+1, h), 
               maxCrossingSum(arr, l, m, h)) 
              
  
# Driver Code 
arr = [2, 3, 4, 5, 7] 
n = len(arr) 
  
max_sum = maxSubArraySum(arr, 0, n-1) 
print("Maximum contiguous sum is ", max_sum)

Chapter 5

Generate a random integer from 3 to 7 using Ransom(0, 1). Make sure the integer will be generated equally in probability.

def Random (3, 7):
    b1 = Random(0, 1)
    b2 = Random(0, 1)
    b3 = Random(0, 1)
    n = convertToInteger(b1, b2, b3)
    if n > 4:
        Random(3, 7)
    return n + 3

algorithm