What is a binary search tree?

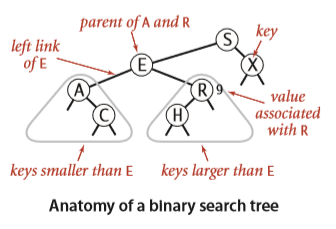
Binary-search-tree property:

Let \(x\) be a node in a binary search tree. If \(y\) is a node in the left subtree of \(x\), then \(y.key \le x.key\). If \(y\) is a node in the right subtree of \(x\), then \(y.key\geqslant x.key\).

public class BST<Key extends Comparable<Key>, Value> {
    private Node root;
    
    private class Node {
        private Key key;
        private Value val;
        private Node left, right;
        private int N;
        public Node(Key key, Value val, int N) {
            this.key = key; this.val = val; this.N = N;
        }
    }
}

Inorder tree walk: print all the keys in a BST in sorted order.

public void inorderTreeWalk(Node x) {
    if (x != null) {
        inorderTreeWalk(x.left);
        System.out.print(x.val);
        inorderTreeWalk(x.right);
    }
}

Theorem 1: If x is the root of an n-node subtree, then the call Inorder-Tree-Walk takes \(\Theta(n)\) time.

Assume: \(T(n)\le (c+d)n + c\)

\[ \begin{equation} \begin{aligned} T(n) &\le T(k)+T(n-k-1)+d\\ &=((c+d)k+c)+((c+d)(n-k-1)+c)+d\\ &=(c+d)n+c \end{aligned} \end{equation} \]

Searching

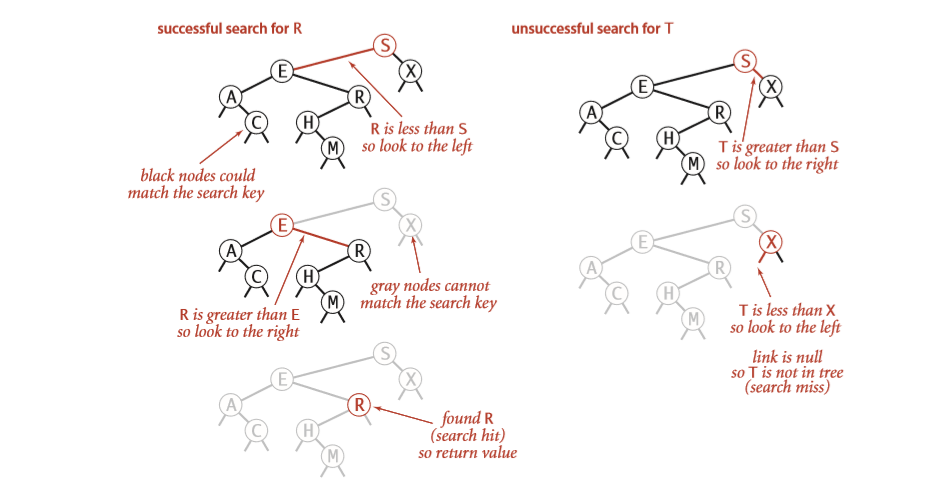
// recursive implementation
public Value get(Node x, Key key) {
    if (x == null)  return null;
    int cmp = key.compareTo(x.key);
    if (cmp < 0)      return get(x.left, key);
    else if (cmp > 0) return get(x.right, key);
    else return x.val;
}

// iterative implementation
public Value get(Node x, Key key) {
    while (x != null) {
        int cmp = key.compareTo(x.key);
        if (cmp < 0)        x = x.left;
        else if (cmp > 0)   x = x.right;
        else break;
    }
    return x;
}

Successor and Predecessor

Successor: the node with the smallest key greater than \(x.key\)

public Node treeSuccessor(Node x) {
    if (x.right != null)
        return min(x.right);
    Node y = x.p;
    while (y != null && x == y.right){
        x = y;
        y = y.p;        
    }
    return y;
}

Insertion

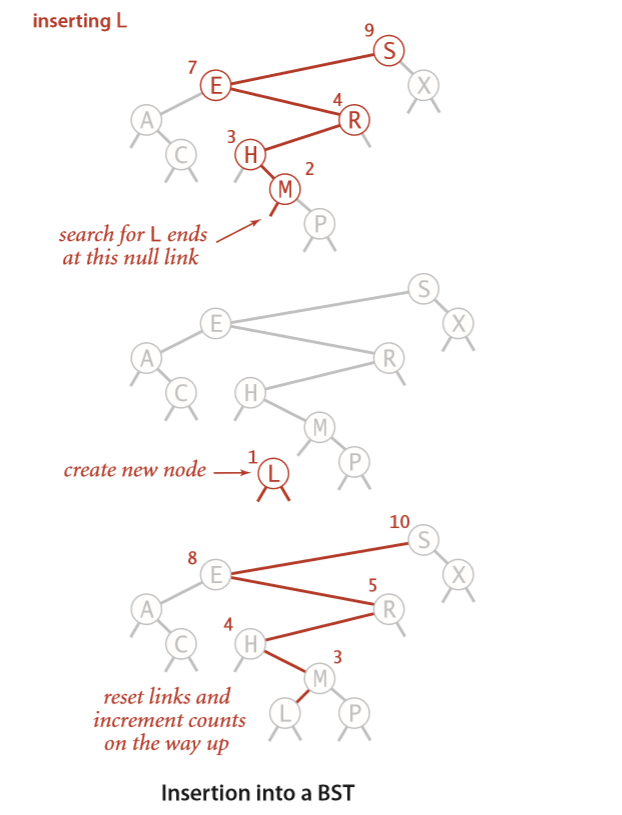
public void put(Node x, Key key, Value val) {
    if (x == null)  return new Node(key, val, 1);
    int cmp = key.compareTo(x.key);
    if (cmp < 0)        x.left = put(x.left, key, val);
    else if (cmp > 0)   x.right = put(x.right, key, val);
    else    x.val = val;
    x.N = size(x.left) + size(x.right) + 1;
    return x;
}

Deletion

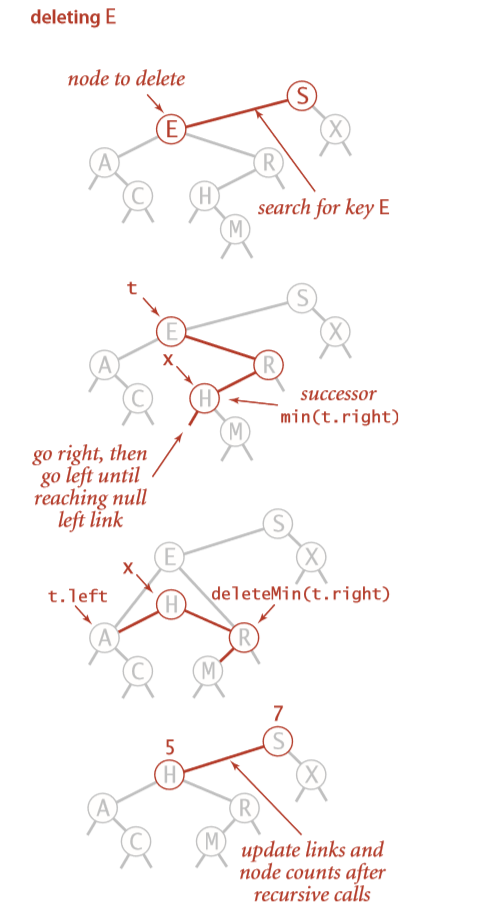
public Node delete(Node x, Key key) {
    if (x == null)  return null;
    int cmp = key.compareTo(x.key);
    if (cmp < 0)        x.left = delete(x.left, key);
    else if (cmp > 0)   x.right = delete(x.right, key);
    else {
        if (x.right == null)    return x.left;
        if (x.left == null)     return x.right;
        Node t = x;
        x = min(t.right);
        x.right = deleteMin(t.right);
        x.left = t.left;
    }
    x.N = size(x.left) + size(x.right) + 1;
    return x;
}

Theorem 2: The running time of INSERT and DELETE is \(O(h)\).

Balanced BST

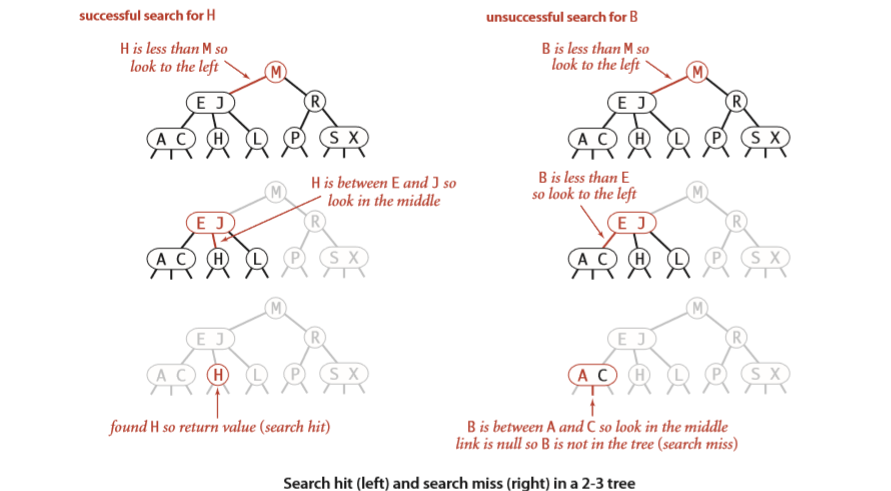
2-3 Search Trees

Property

2-node has one key and two links, \(x.left < x\), \(x.right > x\)
3-node has two keys and three links, \((A,B).left < A\), \(A<(A,B).mid<B\),\(B<(A,B).right\)

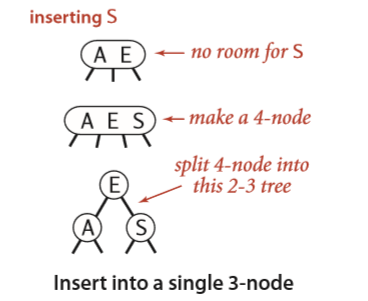
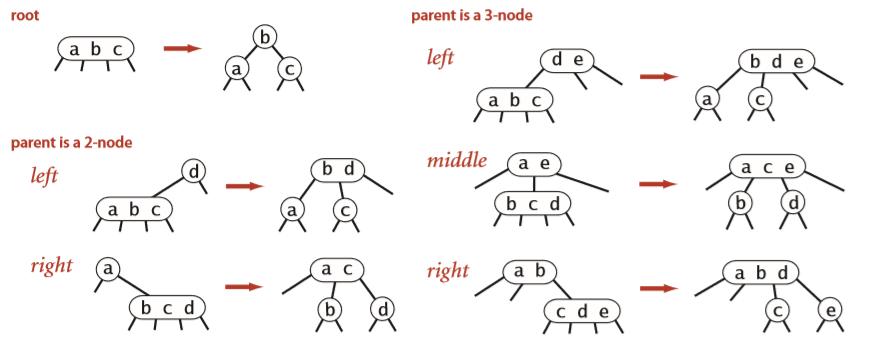
Insertion

Red-Black Tree

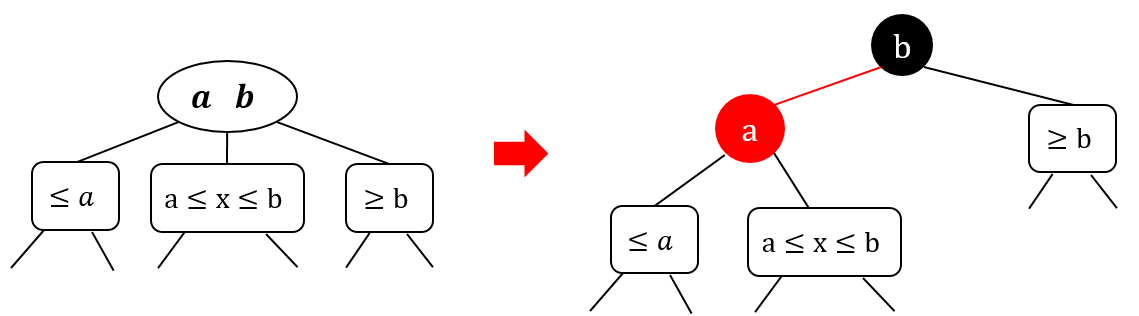
Properties

Every node is either red or black
The root is black
Every leaf is black
If a node is red, then both its children are black
For each node, all simple paths from the node to descendant leaves contain the same number of black nodes

Lemma 1: A red-black tree with n internal nodes has height at most \(2\lg{(n+1)}\)

Proof:

The black-height of the root must be at least \(h/2\); thus, \[ n \geqslant 2^{h/2}-1 \]

\[ \therefore h\le2\lg{(n+1)} \]

Rotation

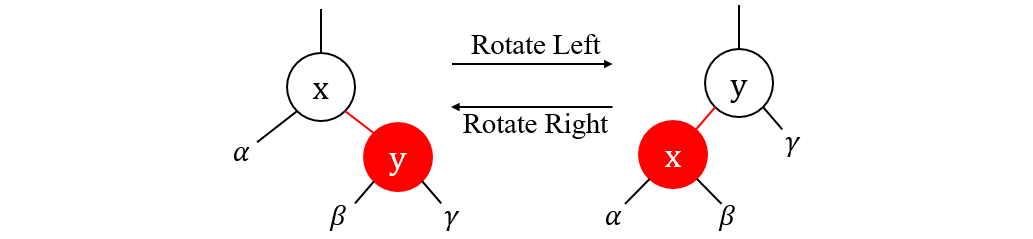
public Node rotateLeft(Node x) {
    Node y = x.right;
    x.right = y.left;
    y.left = x;
    y.color = x.color;
    x.color = RED;
    y.N = x.N;
    x.N = 1 + size(h.left) + size(h.right);
    return y;
}

Insertion

Three Case Insertion

Insert a node \(z\) into the tree. There are three cases in inserting the node into the tree.

case 1: z's uncle y is red

\(y=z.p.p.right\)

Then \(z.p\) and \(y\) become black, and \(z.p.p\) becomes red.

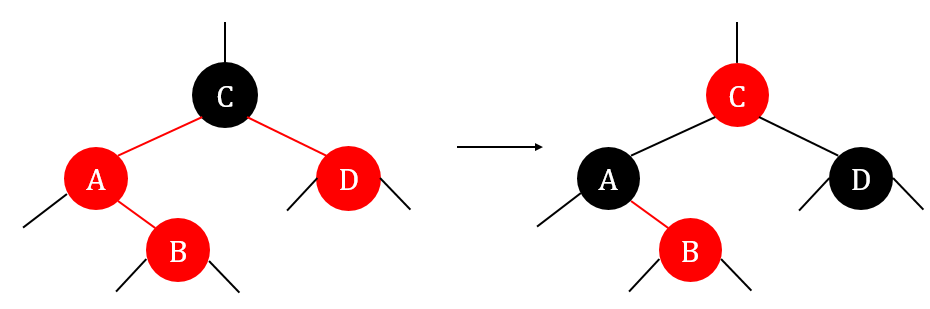
case 2: z's uncle y is black and z is a right child

Left rotate \(z\).

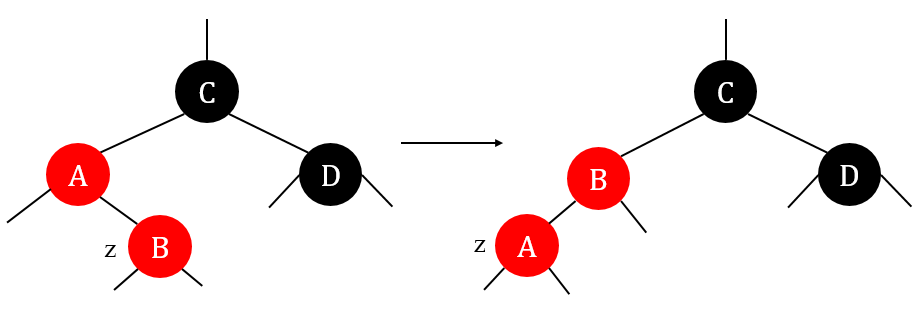
case 3: z's uncle y is black and z is a left child

Right rotate \(z.p.p\) and change color.

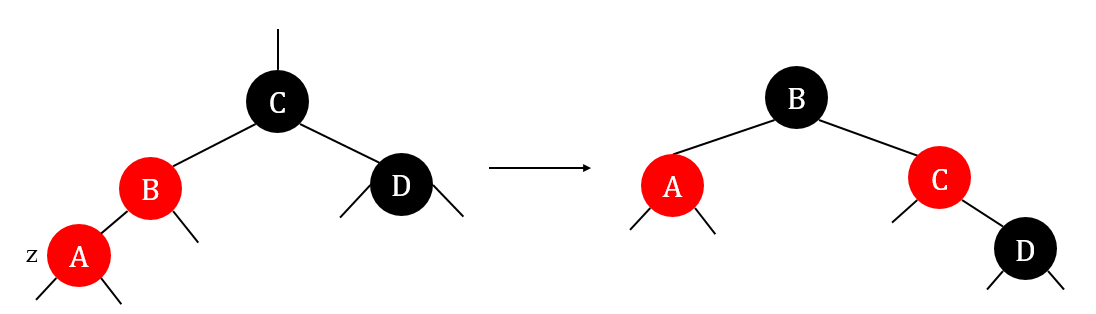
def RB_Insert_Fixup(T,z):
    while z.p.color == RED:
        if z.p == z.p.p.left:
            y = z.p.p.right
            # case 1
            if y.color == RED:
                z.p.color = BLACK
                y.color = BLACK
                z.p.p.color = RED
                z = z.p.p
            # case 2
            else if z == z.p.right:
                z = z.p
                Left_Rotate(T,z)
            # case 3
            z.p.color = BLACK
            z.p.p.color = RED
            Right_Rotate(T, z.p.p)
        else:
            # exchange "left" and "right"
T.root.color = BLACK

Deletion

(Screenshot from the textbook)

def RB_Delete_Fixup(T, x):
    while x != T.root and x.color == BLACK:
        if x == x.p.left:
            w = x.p.right
            # case 1
            if w.color == RED:
                w.color = BLACK
                x.p.color = RED
                Left_Rotate(T, x.p)
                w = x.p.right
            # case 2
            if w.left.color == BLACK and w.right.color == BLACK:
                w.color = RED
                x = x.p
            else if w.right.color == BLACK:
                w.left.color = BLACK
                w.color = RED
                Right_Rotate(T, w)
                w = x.p.right
            w.color = x.p.color
            x.p.color = BLACK
            w.right.color = BLACK
            Left_Rotate(T, x.p)
            x = T.root
        else:
            # exchange "left" and "right"
x.color = BLACK

Reference

[1] Algorithms, 4th edition.

algorithm